Dizionario enciclopedico del calcestruzzo – Sezione 2

Raggi gamma -> vedi Radiazioni gamma.
Radiazioni gamma. Radiazioni per schermare le quali si impiega un calcestruzzo con carburo di boro (<-).

Ramachandran, Vangipuram Seshachar. Nato in India, ha lavorato ad Ottawa presso il National Research Council of Canada dove giunse nel 1968 e diventò responsabile della sezione dei materiali da costruzione dal 1981 al 1991. Prolifico ricercatore sugli additivi chimici sui quali ha scritto come Editor coordinatore anche l’importante manuale “Concrete Admixtures Handbook. Properties, Science and Technology”, Noyes Publication,1995. -> vedi Additivi.

Rame. I sali di rame sono impiegati come materia prima per additivi battericidi (<-).
Rapporto a/c -> vedi Rapporto acqua/cemento.

Rapporto acqua/cemento. Il rapporto acqua/cemento, a/c (<-), è il rapporto tra l’acqua di impasto (<-), a, e il dosaggio di cemento (<-), c, impiegati nel confezionamento del calcestruzzo (<-). Nel calcolo dell’acqua va sottratta quella derivante da un inerte bagnato e va aggiunta l’acqua assorbita da un inerte asciutto o insaturo di umidità: in altre parole, il rapporto acqua/cemento va calcolato con inerti saturi a superficie asciutta (<-) detti anche in S.S.A.

Il rapporto a/c è il parametro composizionale che influenza più di ogni altro le prestazioni del calcestruzzo indurito; in particolare al diminuire del rapporto a/c migliorano:

– la resistenza meccanica a compressione (<-), a flessione (<-) ed a trazione (<-);
– il modulo elastico (<-);
– la resistenza alla penetrazione dell’acqua -> vedi Permeabilità all’acqua;
– la durabilità (<-) con la sola eccezione dell’attacco aggressivo del cloruro di calcio (<-);
– la stabilità dimensionale in relazione alle variazioni causate dal ritiro igrometrico (<-);
– la stabilità sotto carichi permanenti per effetto della deformazione viscosa (<-).

Il rapporto a/c influenza la proprietà più importante del calcestruzzo: la resistenza meccanica a compressione. Su questa correlazione esistono gli studi fondamentali di R. Féret (<-) e quelli che vanno sotto il nome di Legge di Abrams (<-), la teoria di Popovics (<-), e la teoria di Powers (<-) sulla porosità capillare (<-).

Rapporto acqua/legante. E’ il rapporto tra l’acqua di impasto diviso per il legante che include il cemento Portland ed altri materiali cementizi come la pozzolana vulcanica (<-), la cenere volante (<-), la loppa (<-), ecc.

Rapporto d’aspetto. Riguarda le fibre (<-) impiegate nel calcestruzzo fibrorinforzato (<-). Esso è definito come il rapporto tra la lunghezza della fibra e il suo diametro equivalente dove quest’ultimo è il diametro del cerchio di area equivalente alla sezione media della fibra.

Rapporto di iniettabilità. E’ un criterio basato sulla dimensione dei cementi passanti al vaglio di 85 μm e del sistema poroso da iniettare (letto di sabbia o terreno) passante al vaglio da 15 μm per stabilire le probabilità di successo nell’impregnazione del sistema poroso. -> vedi
Microcemento.

Rapporto inerte/cemento. Rapporto tra la quantità di inerte (<-), i, e il dosaggio di cemento (<-), c. Esso condiziona fortemente il ritiro igrometrico (<-) e il calore di idratazione (<-) del calcestruzzo (<-) che diminuiscono entrambi all’aumentare del rapporto i/c (<-).

Rasatura. Malta (<-) di fi nitura applicata sulla superficie di un calcestruzzo indurito (<-) per favorirne l’aspetto liscio.

Rc. Simbolo per indicare la resistenza meccanica a compressione. -> vedi Resistenza meccanica a compressione.

RCC. Acronimo Inglese di Rolled Compacted Concrete -> vedi Calcestruzzo rullato e compattato.
Rck. Simbolo per indicare la resistenza caratteristica (<-) determinata su provini cubici.
Rck pot. Simbolo per indicare la resistenza caratteristica potenziale (<-) determinata con i controlli sui prelievi di accettazione (<-). Coincide con Rck (<-) e deve essere almeno eguale alla Rck prog (<-) prescritta nel progetto.

Resistenza attuale. E’ la resistenza del calcestruzzo in opera che coincide con la resistenza strutturale -> vedi Resistenza caratteristica strutturale determinata per rottura della carota (<-).

Resistenza caratteristica. E’ indicata con il simbolo Rck se misurata su provini cubici (15 cm) ed fck se misurata su provini cilindrici (con altezza/diametro = 2) dove fck vale 0,83•Rck. -> vedi Classe di resistenza del calcestruzzo.

Resistenza caratteristica potenziale. Con il simbolo Rck pot indica la resistenza caratteristica determinata nei controlli di accettazioni sui prelievi di calcestruzzo in corso d’opera che deve essere controllata dal Direttore dei Lavori (<-) o da un suo tecnico di fiducia. -> vedi
Classe di resistenza del calcestruzzo.

Resistenza caratteristica progettuale. Con il simbolo Rck prog indica la resistenza caratteristica indicata dal Progettista e che deve risultare almeno eguale alla resistenza potenziale determinata nei controlli di accettazioni sui prelievi di calcestruzzo in corso d’opera. -> vedi Classe di resistenza del calcestruzzo.

Resistenza caratteristica strutturale. Con il simbolo Rck strutt indica la resistenza caratteristica che deve essere ottenuta nel calcestruzzo della struttura —determinata con prove distruttive (<-) mediante carotaggio (<-) o con prove non-distruttive (<-) — indicata nel progetto e che, secondo le NTC (<-), deve risultare almeno eguale all’85% della resistenza potenziale determinata nei controlli di accettazioni sui prelievi di calcestruzzo in corso d’opera. Questo controllo può essere eseguito dal Direttore dei Lavori (<-) o dal Collaudatore (<-). -> vedi Classe di resistenza del calcestruzzo.

Resistenza meccanica. E’ la sollecitazione (<-) che provoca la rottura del materiale. A seconda della modalità di applicazione della sollecitazione essa si distingue in resistenza meccanica a compressione (<-), resistenza meccanica a flessione (<-), resistenza meccanica a trazione diretta (<-) e resistenza meccanica a trazione indiretta (<-).

Resistenza meccanica a compressione. E’ la più significativa proprietà del calcestruzzo indurito. Concettualmente rappresenta la massima sollecitazione (<-) sopportata da un provino cubico o cilindrico prima di arrivare a rottura per compressione. In teoria la misura è molto semplice poiché si tratta di misurare il rapporto tra la forza (F) capace di rompere per schiacciamento il provino di calcestruzzo, applicata con una pressa in acciaio, e la superficie nota (S) di materiale da provare. Viene indicata con il simbolo Rc (<-) per i provini cubici ed fc (<-) per i provini cilindrici con fc = 0,83•Rc. -> vedi Sollecitazione. In realtà ci sono due aspetti che condizionano il risultato della resistenza meccanica:

1. il tipo di cassaforma, le sue imperfezioni e le modalità esecutive;

2. le interazioni tra modulo elastico (<-) e il modulo di Poisson (<-) del calcestruzzo e della piastra in acciaio della pressa.

1. Modalità di misura della resistenza meccanica a compressione

In realtà la misura della resistenza meccanica a compressione presenta molte insidie se non si adottano alcune regole fondamentali (L. Coppola, “Concretum”, Mc Graw Hill, 2006) con gravi pregiudizi soprattutto nel
contenzioso.
Debbono essere prelevati due provini di calcestruzzo dall’autobetoniera (<-) a metà dello scarico registrando il tipo di autobetoniera, il numero di giri, e il tempo di impasto. I due provini costituiscono un unico prelievo e
la media della rottura a compressione dei due provini rappresenta la resistenza meccanica a compressione del prelievo.
Il prelievo dai getti (<-) dai nastri trasportatori (<-) o dalle benne (<-) va eseguito in tre punti diversi rimescolando le tre pozioni di calcestruzzo.

Il prelievo va fatto alla presenza del DL (<-) o da un suo apposito delegato come imposto dalle NTC (<-). I calcestruzzi dei prelievi vanno costipati a rifiuto con un pestello secondo la UNI 12390-1 fino ad espellere tutta l’aria intrappolata (<-) e raggiungere la massima massa volumica (<-) che corrisponde ad un grado di compattazione (<-), gc, eguale a 1.

Per la preparazione, la forma, le dimensioni e la stagionatura dei provini di calcestruzzo, vale quanto indicato nelle norme UNI 12390-2. Il DL deve redigere un apposito verbale sul prelievo contenente: località e cantiere; numero e sigla del prelievo; composizione del calcestruzzo se nota; data ed ora del prelievo; provenienza del prelievo (betoniera, getto, ecc.).

La scelta delle cubettiere presenta il rispetto di alcune regole; esistono tre tipi di cubettiere: metalliche che possono essere smontate per sformare il provino; in plastica dura di poliuretano espanso riutilizzabili senza essere smontate che presentano sul fondo un foro circolare chiuso da un tappo rimuovibile che viene sospinto dal basso al termine della stagionatura; in polistirolo a perdere per la loro inconsistenza meccanica.
Debbono inoltre essere rispettate le seguenti regole seconda la UNI 12390-2 per migliorare la riproducibilità delle misure:

– le dimensioni effettive del provino cubico (d) non devono variare più dell 0,5% e non più dell’1% se riferito alla distanza tra la faccia superiore non casserata e  quella opposta;
– le planarità delle superfici sottoposte a carico non debbono presentare una tolleranza, maggiore di 0.0006•d;
– la tolleranza sulla perpendicolarità degli spigoli non deve superare 0.5 mm. Per le modalità esecutive secondo la UNI 12390-3 lo sperimentatore deve verificare la planarità delle facce (da sottoporre a schiacciamento) che deve risultare minore di 0.05 mm: se la planarità è superiore lo sperimentatore deve sottoporre i provini a rettifica meccanica.

Occorre inoltre trascrivere i dati del provino (sigla/posizione in opera), misurare con il calibro le dimensioni del provino e trascrivere i valori espressi in mm. Si deve anche pesare il provino prima di posizionarlo tra i piatti della pressa facendo attenzione a centrare il provino nel cerchio disegnato nel piatto inferiore. A questo punto lo sperimentatore accende il motore della pressa e porta il provino a contatto con il piatto superiore. Inserisce quindi la velocità di carico nella pressa che deve essere di 50 N/cm2 al secondo. Al momento della rottura, lo sperimentatore annota il valore della rottura in N/mm2 e il tipo della rottura: 1 = Bipiramidale; 2sb = Sfaldamento piramidale; 2s0 = Sfaldamento obliquo; 3 = obliquo; 4 = Sgretolamento. Dopo aver scaricato la pressa, lo sperimentatore deve riporre il residuo del provino rotto (identificato con la data di effettuazione della prova) sul carrello che verrà successivamente depositato nell’area di stoccaggio del materiale per almeno 20 gg.
Val la pena di segnalare che in molti Laboratori Ufficiali (<-), soprattutto se oberati da un numero rilevanti di cubetti da schiacciare, le misure sopra menzionate non vengono correttamente eseguite per realizzare un maggior profitto a scapito della precisione delle misure.

2. Interazioni tra il calcestruzzo e la pressa in acciaio

La maggior parte delle prove effettuate sul calcestruzzo consistono nel misurare la resistenza alle sollecitazioni uni-assiali di compressione. Tuttavia, anche in queste prove si instaura un sistema piuttosto complesso di sollecitazioni, a causa delle forze di taglio che si sviluppano tra le piastre in acciaio della macchina e le estremità superficiali del provino in calcestruzzo a contatto con esse.

E’ noto che in ogni materiale sollecitato assialmente, e deformato verticalmente, si verifica anche una deformazione laterale di segno opposto; il rapporto, in valore assoluto di questa deformazione e quella verticale è denominato modulo di Poisson (<-). Il modulo di Poisson dell’acciaio non arriva al doppio di quello del calcestruzzo, mentre modulo elastico (<-) dell’acciaio è da 5 a 10 volte più grande di quello del conglomerato cementizio. Questa diversità nei due moduli provoca, durante la prova di compressione uni-assiale, una deformazione laterale dell’acciaio molto più piccola dell’espansione trasversale che il calcestruzzo avrebbe se fosse libero di muoversi. Alcuni ricercatori (K. Newman, L. Lachance, Proceedings A.S.T.M. 64,1044,1964) hanno trovato che la deformazione laterale delle piastre in acciaio è circa il 40% dell’espansione laterale che il provino in calcestruzzo subisce ad una distanza dall’interfaccia acciaio-calcestruzzo sufficiente a rimuovere ogni effetto di contrasto. Infatti, a causa dell’attrito, le piastre dell’acciaio contrastano l’espansione laterale del calcestruzzo nelle parti del provino a contatto con il metallo, ma tale contrasto diminuisce man mano che aumenta la distanza della zona di contatto.

Il grado di contrasto esercitato dalle piastre in acciaio sull’espansione laterale del calcestruzzo, dipende dall’attrito tra i due materiali, ed esso può essere eliminato inserendo uno strato di grafi te o di paraffina tra le piastre ed il provino di calcestruzzo. Quando ciò avviene, si verifica anche una maggiore espansione laterale del calcestruzzo ed alla fine la rottura si manifesta con una spaccatura del provino lungo tutta la sua lunghezza. Quando, invece, l’attrito esiste —come nelle normali condizioni di prova— il provino è sottoposto oltre che alla sollecitazione assiale di compressione ad uno sforzo di taglio, il cui effetto equivale ad una sollecitazione di compressione laterale applicata nelle zone di calcestruzzo a contatto con le piastre come è mostrato nella Figura che segue:

A causa di ciò, in un provino sollecitato uni-assialmente a compressione fino alla sua distruzione rimangono due parti di calcestruzzo relativamente non danneggiate a forma di cono o di piramide con le basi rivolte verso le piastre d’acciaio come è mostrato nella foto della Figura che segue:

La Figura che segue mostra l’infl uenza del rapporto altezza/diametro di un provino cilindrico sulla resistenza meccanica a compressione avendo posto eguale a 1 la resistenza con rapporto altezza/diametro (h/d) = 2.

D’altra parte, nel caso di provini cilindrici la resistenza meccanica a compressione aumenta al diminuire del rapporto h/d, perché si fa sentire maggiormente l’effetto positivo esercitato dallo sforzo di taglio mostrato nella

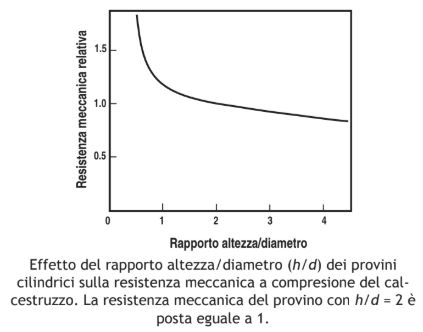
precedente Figura. Ciò dimostra, quindi, che quando lo sforzo di taglio, causato dall’attrito piastra-provino, agisce congiuntamente alla compressione uni-assiale, la rottura del materiale è ostacolata, e che la deformazione laterale, piuttosto che la sollecitazione a compressione, è la causa principale della fessurazione e della rottura. Assumendo per il calcestruzzo un modulo di Poisson di 0,2, l’espansione laterale risulta pari al 20% della contrazione verticale causata da una sollecitazione di compressione uni-assiale. Durante la rottura, le deformazioni unitarie risultano comprese tra 0,003 e 0,004 nella compressione, e tra 0,0001 e 0,0002 nella trazione. Poiché questi ultimi valori sono molto meno del 20% dei primi, ne consegue che le condizioni di rottura a trazione della zona periferica del provino sono realizzate prima che siano raggiunte le deformazioni limiti di compressione.

Per i motivi sopra esposti, quando si debba determinare la resistenza meccanica su provini cilindrici prelevati mediante carotaggio è bene fissare il rapporto h/d eguale a 2 raccomandato da molte normative. Se i provini presentassero un rapporto h/d maggiore di 2 è sempre possibile modificare tale rapporto accorciando opportunamente la lunghezza del provino. Se però il rapporto h/d risultasse inferiore a 2 —per esempio perché lo spessore della struttura risulta relativamente basso rispetto al diametro della carota— è necessario correggere il valore
della resistenza meccanica riconducendolo a quello che si sarebbe ottenuto con un rapporto h/d eguale a 2. Nella Tabella che segue sono mostrati i fattori di correzione, suggeriti dall’A.S.T.M. () e dalle British Standard (B.S.) per i quali occorre moltiplicare i valori della resistenza meccanica.

Se con d si indica il diametro di un provino cilindrico, o il lato della base quadrata di un provino prismatico, l’influenza del rapporto h/d sulla resistenza meccanica del calcestruzzo si applica non solo ai provini cilindrici ma anche a quelli prismatici. L’influenza è naturalmente eliminata se si rimuove completamente l’attrito esistente tra le piastre in acciaio della macchina di prova e le superfici del calcestruzzo con esse in contatto, ma ciò non appare facilmente realizzabile, almeno nelle prove di routine.
Da ciò consegue che a causa del diverso rapporto h/d nei provini cubici ed in quelli cilindrici standardizzati con h/d = 2, lo stesso calcestruzzo può fornire diversi valori di resistenza meccanica a seconda che la misura sia fatta su cubi o su cilindri.
Il rapporto tra la resistenza meccanica dei cilindri e quella dei cubi è ovviamente minore di 1. Le norme inglesi (B.S. 1881 ÷ 1970) suggeriscono di considerare la resistenza meccanica dei provini cilindrici pari all’80% di quella determinata su cubi. Tuttavia, i risultati ottenuti da Evans (R.H. Evans, J. Inst. C.E. 22, 383, 1943-1944) mostrano che il suddetto rapporto può variare tra 0,76 e
0,96 con i valori più alti nei calcestruzzi più resistenti.

Si è spesso dibattuto su quale dei due provini, cilindrico o cubico, sia più adatto per rappresentare la resistenza del materiale. La RILEM (<-) raccomanda, per esempio, di impiegare provini cilindrici in favore dei quali esistono i seguenti vantaggi:

a) minore dipendenza della resistenza all’attrito piastra-provino e quindi maggiore ripetibilità dei risultati;

b) minore dipendenza della resistenza dalla dimensione dell’aggregato grosso;

c) maggiore uniformità nella distribuzione degli sforzi su una superficie piana cilindrica.

I provini cilindrici, inoltre, sono confezionati e sollecitati nella stessa direzione, mentre quelli cubici sono sottoposti ad una sollecitazione assiale dopo aver ruotato di 90° i provini rispetto alla posizione di confezionamento. Ciò significa che nei provini cilindrici la situazione è più simile a quella che si verifica nelle strutture reali. D’altra parte, eventuali fenomeni di segregazione (<-) sono meglio evidenziati nei provini cubici.

Occorre, infine, precisare che, le prove di compressione uni-assiale, indipendentemente dal tipo di provino, non possono rappresentare in modo quantitativo le resistenze delle strutture reali, ma possono solo offrire dei risultati comparativi per valutare l’influenza di un parametro concernente la composizione o la stagionatura del calcestruzzo. Inoltre, la misura della resistenza meccanica a compressione, come anche quella a flessione (<-) o trazione (<-) dipende sensibilmente dalle dimensioni e dalle condizioni igrotermiche del provino oltre che dalla velocità di applicazione del carico.

Il calcestruzzo può essere considerato come un insieme di elementi, ciascuno dotato di una sua resistenza meccanica, nei quali sono casualmente distribuiti un certo numero di difetti. Sotto l’applicazione di un carico crescente la rottura del materiale si innesca in corrispondenza dell’elemento più debole. Aumentando il volume di un materiale da sottoporre alla prova di rottura, aumenta anche la probabilità che il provino contenga un elemento di particolare debolezza, ed appare quindi giustificabile che all’aumento di dimensione del provino corrisponda una diminuzione della resistenza meccanica. Nella Figura che segue è mostrato, per esempio, l’effetto del diametro dei provini cilindrici sulla resistenza meccanica a compressione. Oltre ad una certa dimensione dei provini —50 cm nel caso di questa Figura— l’effetto della dimensione del provino diviene praticamente trascurabile.

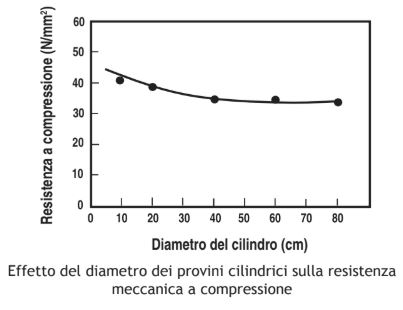
Occorre, d’altra parte, tener conto della influenza della dimensione dei provini sulla dispersione dei risultati ottenuti. Infatti, se la dimensione dei provini diminuisce, aumenta la probabilità che cambi, da un provino all’altro, il numero dei difetti capaci di innescare il processo di rottura. Nella Figura che segue è mostrato schematicamente come varia la distribuzione delle resistenze meccaniche per i provini di due diverse dimensioni: quelli più grandi, pur essendo mediamente meno resistenti, presentano una minore dispersione dei risultati.

3.Influenza dell’UR e della temperatura

L’umidità e la temperatura del materiale al momento della prova, e quindi distinte da quelle della stagionatura (<-), influenzano sensibilmente il valore della resistenza meccanica. Un aumento o una diminuzione di 10°C, rispetto alla temperatura di 20°C, provocano rispettivamente una diminuzione o un aumento del 5-15% della resistenza meccanica a compressione ed a flessione.

L’effetto dell’umidità del provino al momento della prova è un po’ più complesso di quello della temperatura. L’influenza dell’umidità sulla resistenza meccanica del calcestruzzo dipende, infatti, dalla velocità di essiccamento e dalle dimensioni del provino. Un essiccamento rapido e non uniforme del calcestruzzo provoca un ritiro igrometrico (<-) differenziale della pasta cementizia contrastato dall’inerte, ed induce quindi delle sollecitazioni interne di trazione nella pasta. Le microfessure che così si formano innescano il processo di frattura soprattutto nelle prove di trazione e di flessione, ed in minor misura in quelle di compressione. Un rapido essiccamento durante l’esecuzione della prova provoca in sostanza una diminuzione della resistenza meccanica.

Se, però, l’essiccamento avviene molto lentamente ed interessa provini di piccola dimensione, le sollecitazioni interne sono in gran parte ridistribuite e rilassate dallo scorrimento viscoso della pasta. In queste condizioni si è spesso registrato un aumento della resistenza meccanica. Wittmann (F. H. Wittmann, Journal of American Ceramic Society, 56, 409,1973) e Wittmann e Setzer (F. H. Wittmann and M. J. Setzer, Applied Physics, 3, 403, 1974), per esempio, hanno proposto il cosiddetto modello di Monaco per la pasta di cemento secondo il quale la forza di attrazione tra le particelle del gel di cemento (<-) idratato, cioè il C-S-H (<-) aumenta con
l’essiccazione del materiale, per la diminuzione della distanza tra le particelle stesse. Un lento essiccamento provocherebbe, quindi, un ritiro (—Δl/l) ed un aumento di resistenza meccanica (σ—σ0) tra loro correlabili con l’equazione:

(σ—σ0)2 = 1-3•E•Δl / γ0•S•ρl

dove γ0 è l’energia libera superficiale, E è il modulo elastico, ρ è la densità ed S è l’area superficiale specifica. L’aumento dell’acqua tra le particelle provoca in sostanza un aumento della pressione disgiungente tra le particelle di cemento idratate e ne indebolisce il legame, mente il contrario avviene essiccando lentamente il materiale. Mills (R. H. Mills, “Strength–maturity re-
lationship for concrete which is allowed to dry”, RILEM International Symposium on Concrete and Reinforced Concrete in Hot Countries, Haifa, 1960) suggerisce che l’ingresso dell’acqua nel calcestruzzo già indurito porta ad un allontanamento delle particelle di cemento idratato e quindi ad una diminuzione delle forze di coesione.

A causa dell’essiccamento, invece, l’eliminazione delle molecole di acqua incuneate tra le particelle di cemento idratato fa diminuire la distanza tra le particelle e provoca quindi un aumento della resistenza meccanica. L’immersione prolungata in acqua dei provini già essiccati molto lentamente riporta la resistenza meccanica del calcestruzzo al valore ottenuto per i provini stagionati continuamente in ambiente umido, purché il grado di idratazione sia sostanzialmente lo stesso. Da ciò ne consegue che la variazione della resistenza meccanica provocata da variazioni di umidità del materiale è un fenomeno reversibile, purché l’essiccamento sia realizzato così lentamente da non provocare microfessurazioni nella pasta cementizia.

La velocità di applicazione del carico influenza sensibilmente il valore della resistenza meccanica del calcestruzzo. Più lenta è la velocità con la quale aumenta la sollecitazione, più basso è il valore che si registra per la resistenza meccanica. Ciò è probabilmente dovuto all’aumento della deformazione per effetto dello scorrimento viscoso (), cosicché quando si raggiunge un determinato valore critico della deformazione del calcestruzzo la frattura si propaga indipendentemente dal valore del carico applicato. Rispetto ad una prova nella quale il carico è applicato con una velocità di 0,2 MPa/s, si registra una diminuzione della resistenza meccanica di circa il 10-15% quando il carico a rottura è raggiunto molto lentamente, e cioè da 30 min a 4 ore.

D’altra parte un calcestruzzo può sopportare indefinitivamente solo il 70% del carico a rottura misurato applicando una sollecitazione di 0,2 MPa/s. Nelle prove comunemente effettuate in laboratorio, la velocità di applicazione del carico varia tra 4 e 10 MPa/min e la resistenza meccanica può variare del ±3% rispetto a quella ottenuta con 12 MPa/min. L’effetto è particolarmente sensibile quando il carico supera il 50% circa della resistenza a rottura,
mentre è praticamente trascurabile durante la prima metà del carico di rottura.

Sulla base delle considerazioni esposte in questo paragrafo, si evince che la misura della resistenza meccanica valutata attraverso la rottura dei provini non può rappresentare in modo quantitativo la resistenza meccanica delle strutture reali, ma può solo offrire dei risultati comparativi sulle prestazioni dei materiali.

Resistenza meccanica a compressione dei calcestruzzi. Nella Figura che segue è mostrata la resistenza meccanica a compressione media (Rcm) in funzione del tempo (a 1-3-7-28 giorni) e del rapporto acqua/cemento (<-) di 6 calcestruzzi per i cementi di classe 32.5 N -32.5 R – 42.5 N – 42.5 R – 52.5 N – 52.5 R secondo la UNI EN 197-1 (<-).

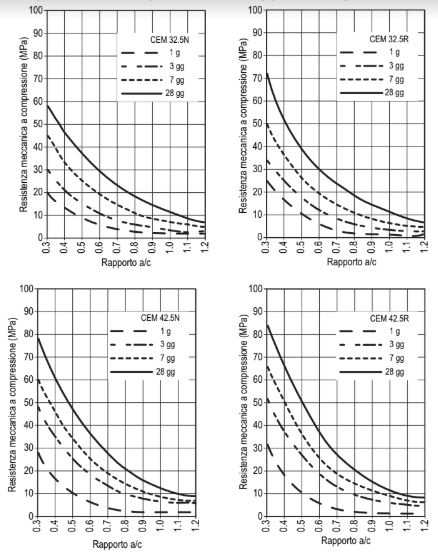
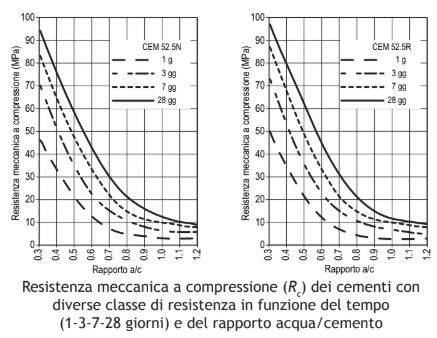
Occorre tener conto che la correlazione tra resistenza meccanica a compressione e rapporto acqua/cemento non segue perfettamente la legge di Abrams (<-) perché come ha notato Popovics (<-) esistono anche altri parametri che influenzano questa correlazione tra i quali i più importanti sono:

– la forma, la tessitura e l’angolarità dell’inerte (<-) che fanno aumentare la resistenza meccanica se la dimensione diminuisce e la ruvidità superficiale aumenta come avviene passando da un inerte tondeggiante e liscio di tipo alluvionale a un inerte di frantumazione;

– il dosaggio di cemento (<-): poiché la pasta di cemento, per la presenza della porosità capillare (<-), è meccanicamente il punto debole del calcestruzzo ordinario, la resistenza meccanica —a parità di rapporto a/c— diminuisce all’aumentare della pasta di cemento, e quindi del dosaggio di cemento c, come appare dalla seguente equazione dedotta sperimentalmente da Popovics (<-) con R in MPa e c in kg/m3:

R = K1 / K2 (a/c + 0.000641 c)

Questa equazione risulta leggermente diversa da quella che segue la legge di Abrams originale dove il dosaggio di cemento non è preso in considerazione:

R = K1 / K2 a/c

A conferma di questa teoria, Popovics ha trovato che nel calcestruzzo con inerte leggero, dove quest’ultimo diventa meccanicamente il punto più debole nel calcestruzzo, la resistenza meccanica R aumenta all’aumen-
tare del dosaggio di cemento c.

Resistenza meccanica a compressione di calcestruzzi con cenere volante silicica. Nelle due Figure che seguono sono mostrate le resistenze meccaniche in funzione del rapporto a/c (<-) quando si un cemento di classe 42.5 R è sostituito dal 10 o dal 20% di cenere volante silicica (<-).