Dizionario enciclopedico del calcestruzzo – Sezione 14
Risalita capillare dell’acqua
Un solido nei confronti di un liquido può presentare due diversi tipi di comportamento: esso può essere liofilo (affine al liquido) o liofobo (nemico del liquido); nel caso in cui il liquido sia, in particolare, l’acqua i due termini diventano rispettivamente idrofilo o idrofobo. Se si considera una superficie piana di solido come un mattone, una pietra, una malta o un calcestruzzo, a contatto con una goccia di un liquido come l’acqua, per la quale mostra un comportamento di idrofilia, l’angolo di contatto θ risulterà minore di 90°C, in quanto la goccia di acqua, per la sua affinità con il solido, tenderà a “schiacciarsi” sulla superficie per estendere al massimo il contatto con il solido, come è mostrato nella parte A della Figura che segue:
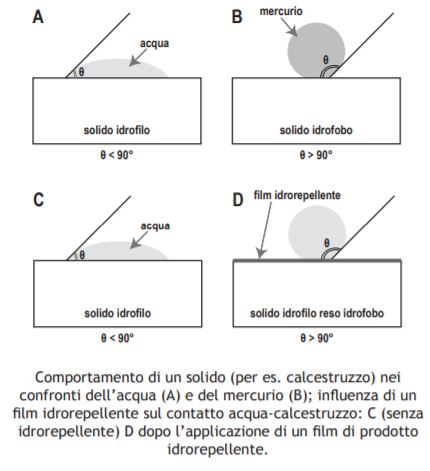
Se invece dell’acqua, il solido è posto in contatto con il mercurio, per il quale esso mostra un comportamento di liofobia, l’angolo di contatto θ risulterà maggiore di 90°C, in quanto la goccia di mercurio tende ad assumere una forma pressoché sferica per minimizzare il contatto con la superficie del solido (parte B della precedente Figura); questo fenomeno è sfruttato nella misura dei pori grazie al porosimetro a mercurio (←). Vale la pena subito di precisare che il comportamento idrofilo di un solido può trasformarsi in idrofobo se la superficie del solido viene trattata con uno strato di prodotti che presenta una repulsione per l’acqua: i silani, gli stearati, i grassi, ecc. sono tipici prodotti da impiegare per rendere idrorepellente la superficie di un solido che di per sé sarebbe idrofilo; in tal caso l’angolo di contatto θ, minore di 90° per una superficie di un solido idrofilo (parte C della precedente Figura) diventa maggiore di 90° per la superficie dello stesso solido rivestita con una pellicola di prodotto idrorepellente (parte D della precedente Figura). Una conseguenza della diversa affinità di un solido per un liquido, e viceversa, consiste nel fenomeno della risalita capillare. Un liquido, che mostri affinità per le pareti interne di un tubo immerso in una vaschetta contenente il liquido stesso (come l’acqua per i pori capillari degli usuali materiali da costruzione), risale spontaneamente all’interno del tubo per suzione capillare (←). E’ come se esso fosse spinto da una pressione (P) così calcolabile mediante la seguente equazione di Washburn (←):
P = (2σ/rc ) • cos θ
dove σ è la tensione superficiale del liquido, rc è il raggio del tubo capillare e θ è l’angolo di contatto.
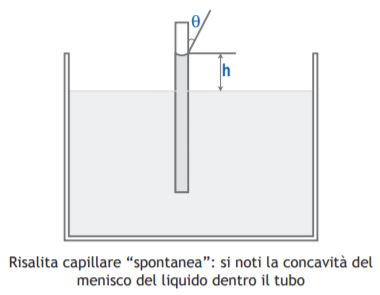
Nel caso di solidi idrofili, cioè con θ minore di 90°, il cos θ è maggiore di zero e la pressione P risulta positiva: è come se la pressione capillare spingesse “spontaneamente” il liquido all’interno del tubo. La pressione P che fa risalire il liquido all’interno del tubo è tanto maggiore quanto minore è rc (cioè quanto più piccola è la dimensione del tubo) e quanto minore è θ (cioè quanto maggiore è l’affinità del liquido per la superficie interna del tubo). La risalita del liquido all’interno del tubo avviene finché, raggiunta una certa altezza h, si stabilisce un equilibrio, espresso attraverso la equazione che segue, tra la pressione capillare (P) che “spinge” in su il liquido dentro il tubo capillare, e la pressione idrostatica (m • g • h) che “spinge” in giù il liquido:
m• g • h = (2σ/rc ) • cos θ
dove m è la massa volumica del liquido e g è l’accelerazione di gravità.
Nel caso di liquidi, come il mercurio, per il quale un solido non presenta affinità, θ risulta maggiore di 90°e pertanto cos θ risulta negativo. Ne deriva che anche il valore di P risulta negativo: ciò significa in pratica, che il mercurio non risalirà “spontaneamente” all’interno del tubo, ma sarà necessario applicare una pressione P sul mercurio per vincere la repulsione del mercurio nei confronti delle superfici interne del tubo liofobe. La pressione da applicare sarà in tal caso tanto maggiore quanto minore è il raggio del capillare e questo principio viene sfruttato nella porosimetria a mercurio (←) per calcolare il raggio un poro attraverso la misura P che occorre per forzare il mercurio in un solido poroso.
Risalita dell’acqua nelle murature in calcestruzzo
La risalita capillare “spontanea” da parte dell’acqua all’interno di un materiale poroso (idrofilo) si verifica nelle murature allorquando queste insistono su una fondazione umida. E’ evidente, almeno in teoria, che la risalita capillare si porterà fino ad una certa altezza secondo la precedente equazione di equilibrio tra pressione capillare che spinge in su il liquido idrofilo e pressione idrostatica dovuta alla gravità che spinge in giù il materiale. L’umidità ad altezze (h) tanto maggiori sarà tanto maggiore quanto minore è la dimensione dei pori presenti all’interno dei materiali. In effetti, la risalita capillare (h) non raggiungerà mai i valori teorici previsti dalla precedente equazione di equilibrio, in quanto una parte dell’acqua che risale può evaporare, a meno che la muratura non sia rivestita su tutti i lati da un rivestimento superficiale impermeabile come è mostrato nella parte sinistra A della Figura che segue:
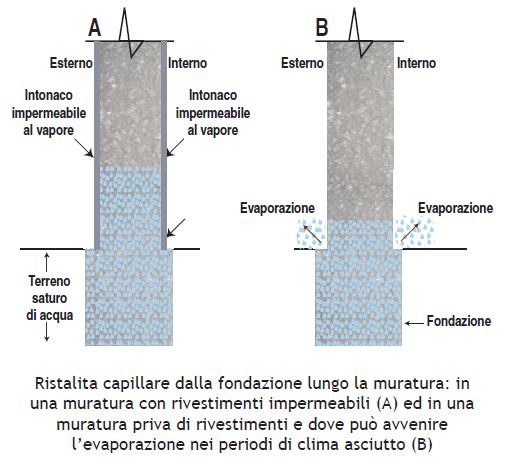
La conseguenza pratica della risalita capillare dell’umidità all’interno delle murature sono molteplici e tutte negative. Innanzi tutto si registra uno scadente comfort interno laddove l’umidità evapora verso gli interni degli edifici (parte B della precedente Figura). In secondo luogo l’acqua presente nelle murature può congelare d’inverno ed innescare un degrado del materiale in conseguenza della formazione ciclica e distruttiva del ghiaccio. Infine, se l’acqua contiene sali idrosolubili, si possono innescare fenomeni di cristallizzazione salina discussi nel sottostante paragrafo intitolato “Efflorescenze e sub-florescenze”.
Equilibrio igrometrico fondazione-muratura-ambiente
La massima risalita (h) di acqua per capillarità è ricavabile dall’equazione che segue nota come legge di Jurin (←):
h = 2 σ • cos θ / (rc • m • g)
dove m, la massa volumica dell’acqua, è 1000 kg/m3 , g vale 9,81 ms-1, e σ è la tensione superficiale ed è uguale a 72 · 10-3 N · m-1. Per un liquido come l’acqua che bagna bene i materiali da costruzione (calcestruzzo incluso) θ = 0 e si ottiene:
h = 14,7 • 10-6 / rc
In base alla precedente equazione si deduce che in un materiale poroso costituito solo da pori con raggio capillare rc di 1 μm = 1·10-6 m l’altezza di risalita dell’umidità dovrebbe arrivare al massimo a circa 15 m secondo la seguente equazione:
h = 14,7 • 10-6 / 1 • 10-6 = 14,7 m
La porosità capillare di molti materiali che si trovano nelle varie costruzioni presenta una distribuzione dimensionale dei pori compresi tra 0,1 e 10 μm (mostrati nella Figura che segue), e pertanto per risalita capillare l’acqua potrebbe teoricamente raggiungere un’altezza nella muratura anche oltre 15 m.
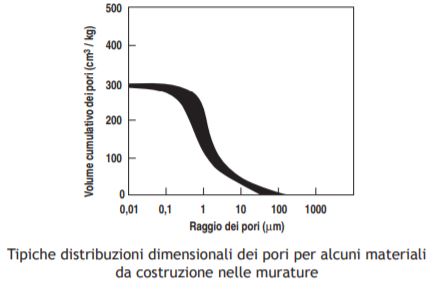
In effetti, anche in murature costantemente insistenti su un sottofondo bagnato, difficilmente si registrano risalite capillari oltre i 2-3 m. La ragione di questa discrepanza tra teoria e realtà sta nel fatto che, accanto al fenomeno della risalita capillare, coesiste, come già si è detto, quello dell’evaporazione dell’acqua attraverso le superfici non protette Inoltre, la risalita capillare richiede del tempo (come è mostrato nella Figura che segue): inizialmente essa procede con una velocità lineare di circa 2 cm/ora ma successivamente la cinetica di risalita è molto più lenta. Tuttavia, l’aspetto cinetico del fenomeno è praticamente annullato, dopo qualche anno, laddove, le murature insistono su fondazioni che sono perennemente immerse in acqua; l’aspetto cinetico deve essere, invece, preso in considerazione laddove la bagnatura delle fondazioni è discontinua o addirittura occasionale.
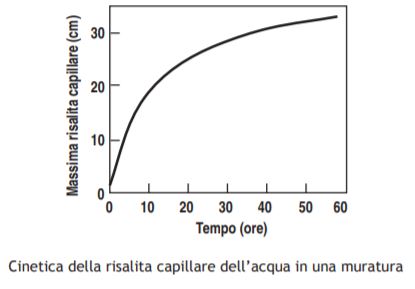
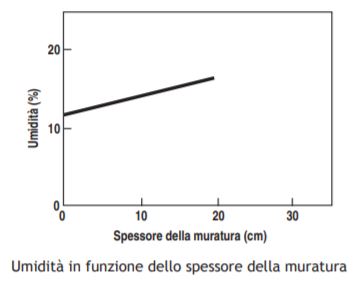
Ritornando all’influenza dell’evaporazione dell’acqua (dalla parete esposta all’aria) sul contenuto residuo di umidità risalita per capillarità nella muratura, la Fig. che segue illustra quale è un tipico diagramma altezza-umidità in una muratura in cui coesistono la risalita capillare della fondazione e l’evaporazione dell’acqua dalla parete. Si osserva che il contenuto di acqua può raggiungere valori del 20-30% nelle zone basse della muratura fino a circa 1 m. Per altezze superiori, l’evaporazione dell’acqua dalla muratura annulla in gran parte l’alimentazione dell’acqua per risalita capillare e si registra una diminuzione brusca del 15-20% fino a circa il 5% nella fascia di muratura tra 1 e 2 m di altezza. Per altezze della muratura superiore a 2-3 m, il valore dell’umidità residua (valore “a”sull’ascissa della Figura che segue) non è tanto dovuto alla risalita capillare, quanto invece alla condensazione capillare ed il valore di a (circa 2-3%) dipenderà ovviamente dall’UR ambientale e dalla dimensione dei pori in accordo alla legge Kelvin-Wheeler. Ovviamente la forma precisa della curva illustrata nella Figura precedente nei vari casi specifici dipenderà dal tipo di muratura, dalla costanza o meno di alimentazione di acqua dalla fondazione e dalle particolari condizioni micro-climatiche (vento, UR, temperatura, insolazione) che potranno favorire o meno l’evaporazione dell’acqua.
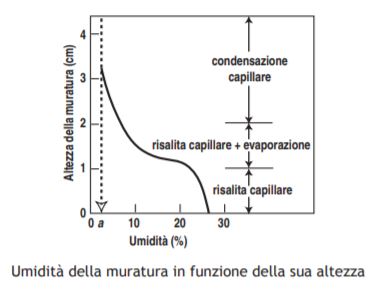
Per quanto concerne l’umidità nella muratura a parità di altezza, essa varierà solo leggermente in funzione dello spessore della muratura e tenderà ad essere leggermente inferiore verso la parete da dove avviene l’evaporazione come è mostrato nella Figura che segue: